“When a person with experience meets a person with money, the person with experience gains money and the person with money gains experience.” Anon.
“Our strategy is to get big fast.” Jeff Bezos of Amazon.com
Twenty-first century economic winners are those that find non-equilibrium business opportunities. Economics, the so-called dismal science, has been focused on supply and demand equilibrium conditions since the 18th century, but that is not how people generally make money. Money is made during that dynamic transient when the equilibrium is upset. As a generally theory, focusing on equalibria is fine (like a course on statics in engineering), since most businesses in fact don’t make much money, but as an executive, your goal is not to partake of the profitless commoditized equilibria that characterize so much of the world, but rather to find those discontinuities, differentiations, and non-equilibrium situations where it is possible to make outsized profits. Indeed, when people talk about innovations in business, there is almost always some violation of the static condition. In this essay I want to focus on one of the thousands of ways to move off the status quo, that is, to move down the virtuous path of learning faster than your competition. If you have more market share than your competitors then there are two huge advantages you can enjoy if you manage your business well. One is economies of scale and the other is the experience curve effect. In economies of scale, one gets to amortize fixed costs over a larger revenue base. To take a contemporary example, Sarbanes-Oxley compliance is a huge cost for US public companies which is relatively more expensive for $50M per year companies than $5B per year companies. Economies-of-scale come from the pure effects of scale. The other type of advantage comes from the experience curve, which states that, if you are doing the job right, every time you double the cumulative output of your organization will get some percentage more efficient.
According to Wikipedia, the learning curve was first discovered by 19th century German psychologiest Hermann Ebbinghaus and later quantified in 1936 by Wright-Patterson Air Force Base.
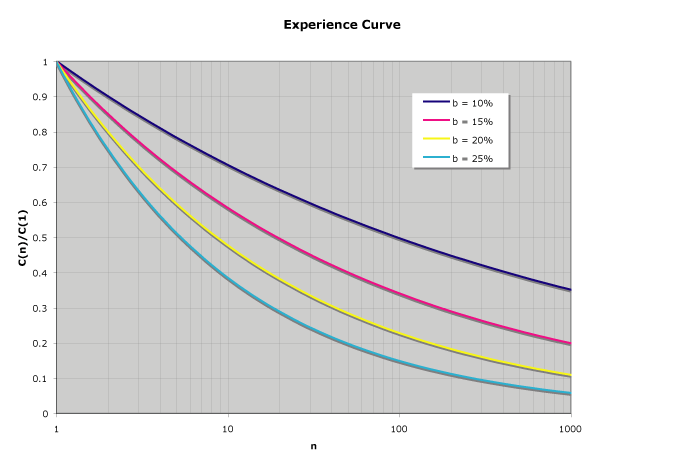
Typical improvements, b, are in the 2-30% range for every doubling of cumulative production. This would correspond to a 98-70% experience curve. Mathematically, if n is the number of cumulative units produced, then the cost C of the nth unit is given by
C(n) = C(1) nlg(1-b)
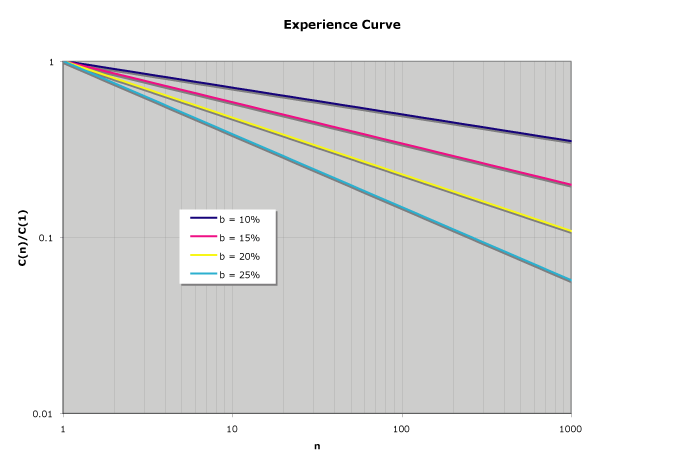
where lg(x) is log base 2 of x and b is benefit of the experience of doubling of output. Thus for b = 15%, 2lg(1-b) = 1-b = 0.85 = 85%. The experience curve looks like this (which is a lot like Moore’s Law. . . ):
or
Let us examine two companies, ExCo and WhyCo where ExCo’s market share is x and WhyCo’s market share is, of course, y. Let us assume that they are both selling into the same market and that that market sets the price ASP. The profit PFO is given by
PFO = ASP – C,
which is true for both companies, but because they have different market share, their costs are different. Assume that the companies learn at the same rate b, sell at the same price ASP, and have held their relative market share since the beginning. Furthermore, let the cumulative served available market be CSAM. In this case, for ExCo we have
PFOx = ASP – Cx = ASP – CSAMlg(1-b) xlg(1-b)
And for WhyCo
PFOy = ASP – Cy = ASP – CSAMlg(1-b) ylg(1-b)
The difference is profit is
PFOy – PFOx= CSAMlg(1-b) [xlg(1-b) – ylg(1-b)]
Let the ratio r of the marketshares of WhyCo to ExCo be
r = y/x.
The ratio of costs for WhyCo and ExCo are
Cy/Cx = (y/x) lg(1-b) = r lg(1-b)
Or
Cx/Cy = r -lg(1-b)
Assume that ExCo’s market share is greater than that of WhyCo. If we assume that ExCo and WhyCo are the only participants in the market, then x + y = 100%. As a function of learning or experience curve we have
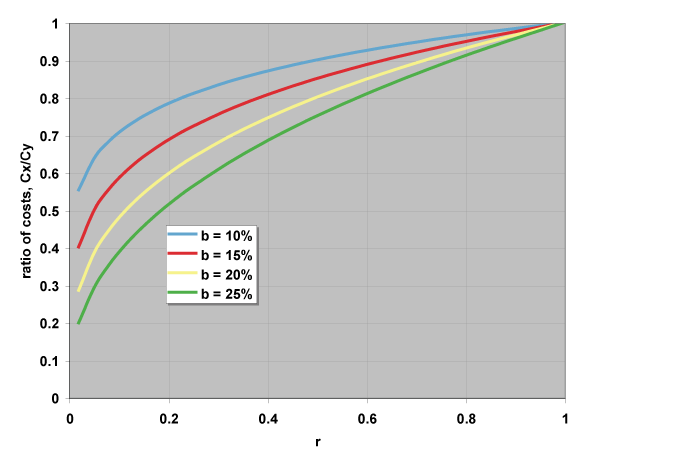
Lower costs are, of course, good.
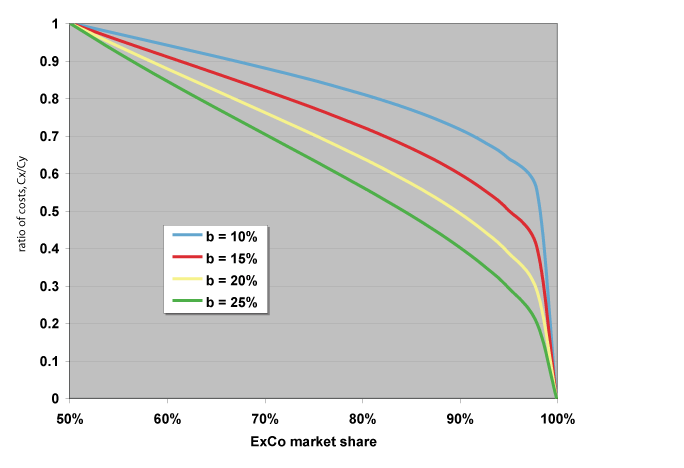
Note how nonlinearly this curve behaves at very high market share. In general, y < 100% – x, meaning that r should be interpreted as the ratio of the market shares of the second-largest vs. largest competitors.
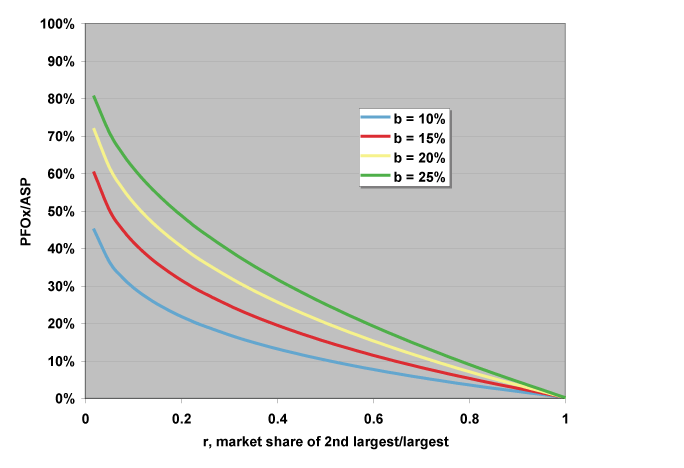
There is another interesting case. Assume that the PFO of WhyCo is zero (I wonder how that would happen, eh?). In that case the profitability of the ExCo is given by
PFOx/ASP = 1 – r-lg(1-b)
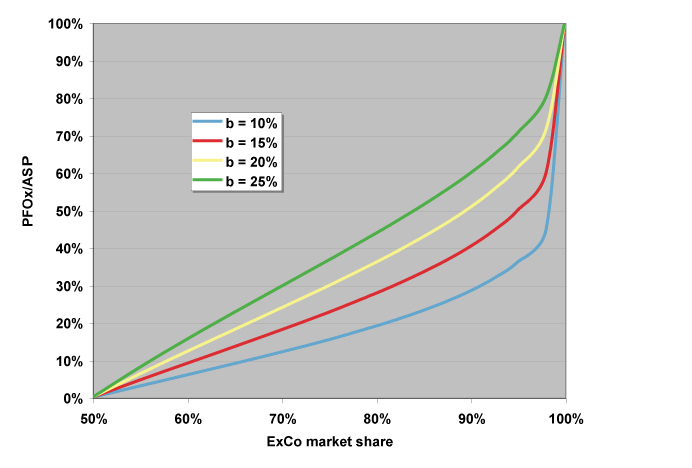
This is obviously idealized since the ASP cannot rise unboundedly. There will be substitutes, if only that ubiquitous competitor, “do nothing.” Nevertheless, commanding market share can extract very high rents. Notice that such as situation is self-perpetuating, at least until something else comes along to disturb the situation. Of course, something else always comes along, eventually. The results are plotted below.
or
Bain and Company like to plot this curve this way:
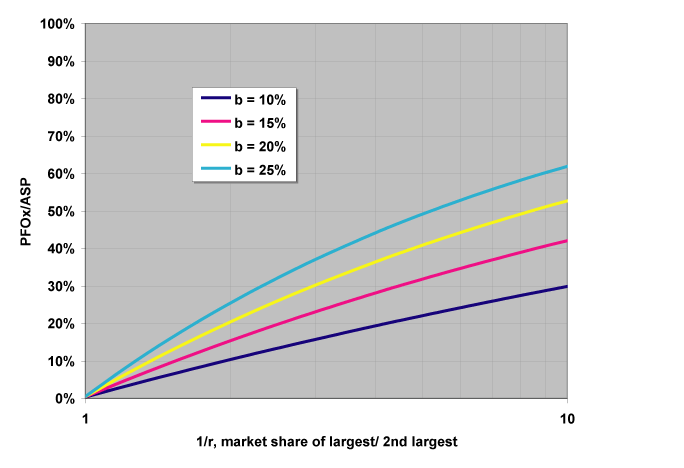
However you slice it, larger market share translates to higher profits when two companies learn at the same rate. This effect is accentuated when the experience or learning curve effects are relatively more important. Many strategies have been based on these effects where one sees companies jockeying very hard for early marketshare so as to take advantages of this virtuous dynamic.
Every theory has limitations and sometimes it is at least as important to examine the assumptions as to grind through the math. In this case the most important assumption is that the learning rates of the combatants are equivalent. In reality different companies learn at different rates and there are numerous factors that affect these rates, many of which are influenced by management. Intel offers a good case study. At the time they exited the dRAM business it was widely believed that a semiconductor company needed to be in dRAM manufacturing because dRAM’s were the high-volume learning vehicle that drove improved process capability and cost structure. Intel rejected this hypothesis and methodically created a company that could learn very well indeed on microprocessors. (And this was before microprocessors had the huge on-chip memories that they sport today.)
How are you going to learn faster than your competition?