Business
Founder and CEO of ExXothermic, a pioneering company in Wi-Fi Audio Streaming with applications in Fitness, Hospitality, and Assistive Listening. Acquired by Listen Technologies in April 2020.
Founder and CEO of GX3 Innovations, a DARPA-funded R&D organization specializing in national security products and services.
CTO at KLA-Tencor: Responsible for oversight of KT’s $330M annual R&D budget. Created KT Labs. Set company Design for Manufacturing (DFM) strategy. Responsible for external funding for KT for the last few years and brought in tens of millions per year from the government.
Group VP for Wafer Inspection at KLA-Tencor: Head of corporate operations. 2004-2005 Responsible for $1B in annual revenue. Exceeded all financial targets. Was the most profitable Group in the company in terms of percentages and dollars. Created KT’s first Global Operations organization, which produced about $2B/yr revenue. Initiated the company’s first substantial Asian offshore manufacturing project. Re-organized to drive our first projects to use design automation information in wafer inspection.
VP/GM RAPID (Reticle And Photomask Inspection Division) at KLA. 1999 – 2004 Doubled revenue to over $300M while decreasing HC 40% and cutting cycle-time by 35%. Created as much profit in my second full year as GM as in all of the previous decade; also generated a tremendous amount of cash flow, not only driven by profitability but also by significant reductions in invested capital. Introduced two successful product generations (with < 1% excess and obsolete). Raised prices by 2-3x while increasing market share to over 90%. Rationalized the product line down to half the number of subsystems and created a product family where customization could be done very late in the manufacturing cycle, resulting in the most profitable division in the company. Introduced war-gaming to KT. Drove Nikon out of the business and held competitors NEC, Toshiba, Applied Materials to about one sale per year each. Launched the DesignScan design automation business.
Member of the Board, D2S (IP & electronic design automation) for 10 years. Now member of the Board of Listen Technologies.
Technology
I started my professional career as a microwave circuit designer and, over my career, have designed circuits and performed advanced electronics research from dc to daylight. My experience includes microwaves, picosecond optics, digital MOS VLSI, semiconductor device fabrication, superconductivity, computer-aided design, circuit theory, and computer engineering.
The broad theme is high-performance circuits. Out of a medley of lesser accomplishments, the five of which I am most proud are (1) being the first to modelock the cw semiconductor laser, (2) my book, with Mr. Dan Dobberpuhl, on digital VLSI circuits, (3) theoretical work on the natural frequencies of linear circuits, (4) investigations of the superconducting transistor, and (5) invention of a new class of multiport memories.
In 1978, I was a member of the M.I.T. team that first modelocked a cw semiconductor laser. The team included P.-T. Ho, E. Ippen, and my thesis advisor, Prof. Herman Haus. We achieved pulse widths in the 20 ps range—two orders of magnitude faster than earlier attempts. The repetition rate was a few GHz, a first for any laser system. We succeeded with GaAlAs and then with GaInAsP. Three years later, conferences were holding entire sessions devoted to the modelocking of semiconductor lasers.
In 1980, I joined the M.I.T. EECS faculty with the mission of helping that institution achieve world prominence in VLSI. This lead to my second significant accomplishment, a widely referenced book on digital MOS VLSI circuits used at nearly all leading engineering institutions in the world. It was primarily in recognition of this work that I received, in 1986, the Frederick Emmons Terman Award. Fredrick Emmons Terman Award, EE Div, ASEE, June 1986
In 1986, I was inspired by Professors John Wyatt and Paul Penfield to apply circuit theory to a problem that has bothered me since my early microwave plumbing days, how can one look at the characteristics of a device, such as a four-terminal transistor, and discover how fast it will be in an optimal circuit? What are the figures of merit that can be effectively applied to transistors as well as laser diodes? In this classic problem, I was the first to achieve tight performance bounds. Now one can look at a catalog of linear components, replete with parasitics, and predict exactly what natural frequencies (e.g., the maximum frequency of oscillation) can be realized by components ordered from the catalog and optimally connected. An optimal synthesis is also given.
In the fall of 1987, I went to Hitachi Central Research Laboratories, in Tokyo, to be the first circuit designer to look at modeling and circuit aspects of the superconducting field-effect transistor. A careful investigation of the existing models proved to me that they were thermodynamically unsound. This lead me to predict a possible new physical phenomenon—the magnetic flux-controlled gate voltage effect.
After returning from Japan, in 1989 I invented a two-port RAM using single-port cells that exploits the practice of storing words rather than just bits in a memory array. By arranging words in memory in an unorthodox manner one can assure that any two words, simultaneously read to different memory ports from single-port cells in the array, conflict in at most one bit position. Any error produced can be corrected after examining the parity of the words, resulting in perfect operation in all cases. Galois-field arithmetic was used to calculate addresses. The invention was generalized to a new class of multiport memories and patented.
One award-winning book on VLSI; 40 technical papers and 33 granted patents in half a dozen technical fields. Spans hardware and software.
M.I.T. Ph.D. EECS June 1979. U. Mass Amherst B.S. ECE/Honors June 1974 (Magna Cum Laude). Outstanding Alumni Award, Univ. of Mass. College of Engineering, May 1994
Assistant, then Associate Professor of Electrical Engineering and Computer Science 1980-1988. Taught, researched, and practiced the art of integrated-circuit design, including the architecture and implementation of integrated systems; computer-aided design; and optical, superconducting, and electronic devices. Wrote, with Dan Dobberpuhl, The Design and Analysis of VLSI Circuits.
Visiting Senior Researcher at Hitachi Central Research Labs 1987-1988 in the newly invented area of high-temperature superconductors. Discovered a new physical phenomena: flux-controlled voltage in charge-controlled Josephson Junctions.
CTO KLA-Tencor
Public Service
Multiple DARPA positions, including Director of the DARPA Electronics Technology Office (R&D budget $500M/year). In the early 1990s developed the strategic thrust that was mobile information systems connected to information networks.
Sold over a billion dollars in programs to DoD and Congress. Initiated and managed multiple programs, many of whose results have entered the mainstream, including low power electronics and microarchitectures, various optical communication techniques, blue lasers, computer-aided design, MEMS (micro-electromechanical systems), bio-MEMS, advanced packaging, microwaves, signal processing, etc.
Co-founded the International Electronics Manufacturing Initiative (iNEMI)
Wrote, with Dan Dobberpul, the Design and Analysis of VLSI Circuits
Art
I have always been drawn to figurative art, especially when gesture and motion are the dominant themes. His bronze sculptures have a fluidity of line that belies their solidity. I’m always thinking about the rhythm of the finished piece. Finding the lines of motion is the only way I know to make a piece of bronze imply movement.
Always striving for nuanced effects, I incorporate textures and patinas that suit each subject and concentrates on facial expressions that fit the milieu of each subject.
My dynamic bronzes have won multiple awards and are included in numerous collections around the world. I was born in the Year of the Dragon and note that that could explain my penchant for fantasy elements in my work. I challenge the the viewer to find the twist in each of my works of art.
You will see examples of my art connected to most of the blogs posted here. Why should a tech or business post have a picture of a bronze sculpture or a charcoal and chalk drawing? Because they come out of the same brain, so why not? Compartmentalization is over rated.
Fiction
I have started to play with writing fiction. My wife loves this because finally I have a hobby that does not make a mess in the house.
My first attempt was a story about aliens and AIs. The plot line is struggling but I have been having a lot of fun thinking about world building. You can read about Zero’s story here.
I have also scanned some copies of Betelguese from the early 1970s. It is the U Mass Science Fiction Society fanzine. You can check it out here.
Blog
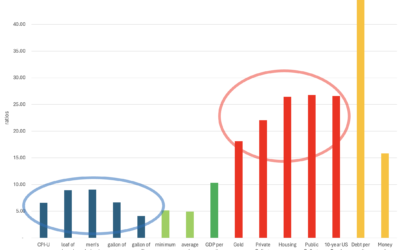
Debt, Inflation, and Debasement
The United States spends more than it produces and pays for the difference with debt. This causes inflation. Historically, countries take on debt to fight wars and sometimes to ease the effects of a recession. Today, as a nation, we seem addicted to debt in bad times...
Sculpture and AI
Yes, AIs can sculpt. They already have. Sculpture and AI are going to live together from now on.
How to mount a bronze sculpture to a base
This is a blog on how to mount a sculpture to a wood or stone base when the tapped holes are hidden. There is a trick to knowing where to drill the mounting holes so that they line up. I will show this step by step, with photos.
Chetna Meets a Feral AI
“Knock, knock. Please don’t kill me.” came the single-packet data squirt from MAC address 3c:22:fb:45:78:5d. The AI located the sender in an Ohio nursing home.
50 Rules for Amazing Figurative Sculpture
Below is a list of 50 rules for figurative sculpture, with an emphasis on using plasticine clay and targeting a bronze finished product. I have collected these rules over decades from teachers, books, and clay-under-finger-nails experience. To see my sculptures,...
Two PhDs read a book on whitewater canoeing and drive to Maine
Two PhDs read a book on whitewater canoeing on their drive north to Maine. What could go wrong?
Contact Us
We look forward to hearing from you for everything from art to technology to business to life.
I hope you hug the people that want to hug you. That you have adventures that make you feel alive. That you end the year feeling even more vigorous than you start it. That you learn new things that are true.